|
заместитель директора ИЭ УрО РАН, д.э.н., Шматов Г.А., с.н.с. УрГУ, к.ф-м. н
В статье обосновывается применимость аналитических методов для решения задач эффективного размещения рекламы. Излагаются основные принципы количественной теории медиапланирования, позволяющей решать задачи оптимизации рекламного бюджета при размещении рекламы в СМИ. Показано, что аналитический аппарат теории дает возможность прогнозировать все практически важные количественные характеристики медиапланов, обходясь при этом минимальным набором данных измерений.
Введение
Решать задачи планирования рекламы приходится каждому специалисту, связанному с размещением рекламы. При планировании рекламы любой специалист неизбежно сталкивается со следующими вопросами:
- какая часть аудитории будет охвачена рекламой,
- какая её часть будет охвачена тем или иным медиа,
- сколько контактов с рекламой в среднем будет иметь представитель аудитории,
- какое количество СМИ нужно выбрать для рекламы,
- сколько нужно сделать выходов рекламы в каждом из выбранных медиа,
- с какой периодичностью нужно проводить рекламные кампании.
Все эти вопросы могут быть решены только на основе адекватной количественной теории. При этом теория должна быть такой, чтобы её результатами могли пользоваться не только специалисты рекламных агентств, но и менеджеры по рекламе любых фирм. Как сказано в классической книге по медиапланированию Дж. Сиссорса и Р. Бэрона, «…специалист в области медиапланирования использует статистические данные с целью доказательства того, что в план включены лучшие средства распространения рекламы, позволяющие охватить всех потенциальных покупателей» [1], c. 34.
Теория медиапланирования и занимается разработкой таких доказательств. С помощью оптимального размещения достигается минимизация рекламного бюджета и максимизация эффекта рекламного воздействия.
В изданной на русском языке литературе практически отсутствует материал, относящийся к разработке количественной теории медиапланирования, понимаемой как оптимизация размещения рекламы. Поскольку медиапланирование относится к количественным наукам, его основные понятия и параметры формулируются на математическом языке. Один из классиков рекламы, К. Хопкинс, подчёркивал: «наиболее убедительные аргументы при рассмотрении рекламных планов — это цифры» [2], c. 78. Анализ литературы по количественным аспектам медиапланирования приводит к неутешительным выводам. Несмотря на обилие литературы по рекламе, публикаций, в которых были бы подробно изложены количественные основы планирования и оптимизации размещения рекламы, практически нет. В учебниках и монографиях по рекламе подробно описываются методы, используемые на этапах стратегического и тактического планирования рекламы [1, 2, 3, 4, 5, 6, 7, 8, 9]. Однако количественным методам оптимизации рекламного бюджета и размещения рекламы уделяется совершенно недостаточное внимание. Например, описанию программ по медиапланированию в книге Р. Батра и др., содержащей 780 страниц текста, уделено только две страницы, [5, с. 623—624]. В специальных публикациях решены отдельные частные задачи, которые невозможно использовать в практической работе большинства отечественных менеджеров по рекламе. Это связано, в основном, с неполнотой и фрагментарностью представленных в публикациях методов. Работы основаны на подходах, требующих данных, технологий и ресурсов, недоступных большинству отечественных пользователей.
В отечественной литературе по медиапланированию приводятся, как правило, определения терминов, используемых в медиапланировании, и даётся описание общих принципов планирования рекламы [10, 11, 12, 13]. При этом в части этих публикаций описываются некоторые программные продукты по медиапланированию, но только на уровне пользователя, без описания алгоритмов, на которых они основаны [12]. В тех книгах, где имеются элементы количественной теории, как правило, приводятся лишь две-три формулы, к тому же без обоснования и часто с ошибками, см., например, [10], с. 44; [13], с. 80. Отметим в этой связи, что во многих областях менеджмента, маркетинга и маркетинговых исследованиях математические методы анализа используются весьма широко, см. напр., [14]-[18].
Нами поставлена цель восполнить указанный выше пробел в литературе по рекламе и изложить основные принципы количественной теории медиапланирования.
Медиапланирование и медиаисследования
Прежде чем излагать основы теории, необходимо остановиться на некоторых общих вопросах, поскольку медиапланирование — это только один из этапов создания рекламной кампании, являющейся, в свою очередь, лишь элементом маркетингового комплекса управления. Как отмечали Дж. Сиссорс, Р. Бэрон? «Процесс медиапланирования всегда предваряется маркетинговыми соображениями» [1], с. 28. При разработке маркетинговой и рекламной стратегий необходимо соблюдать основополагающие законы, принципы и правила, сформулированные профессионалами в области создания эффективной рекламы, такими как К. Хопкинс, Д. Огилви, Ф. Котлер, Р. Ривз, Э. Райс, Дж. Траут, Д. Аакер, Д. Шульц, Р. Лаутерборн, Э. Эфрон, Дж. Джоунс, Дж. Росситер, Л. Перси, П. Дойль, А.Лебедев, В.Зимин, А.Мирошниченко. Суммируем сделанные этими специалистами заключения в виде трёх наиболее важных законов:
- постановка маркетинговых и рекламных задач, основанных на запросах и возможностях потребителя (маркет-менеджмент);
- использование данных маркетинговых исследований на всех этапах создания рекламы;
- научный подход к рекламе.
Без соблюдения этих законов нельзя сделать рекламную кампанию эффективной, опираясь только на оптимальное размещение рекламы или удачное творческое решение. Вопросы стратегического планирования подробно рассмотрены в обширной литературе ([1, 2, 3, 4, 5, 6, 7] и ссылки в них).
Для оптимизации размещения рекламы используют данные, полученные в результате медиаисследований, и компьютерные программы, извлекающие нужные параметры из специальной базы данных (массива данных), полученных в результате опросов. В большинстве используемых методик упор делают именно на извлечение медиапараметров из базы данных (охваты отдельных СМИ и их сочетаний; охваты, соответствующие различному числу контактов). Оптимизация размещения заключается в поиске такой комбинации выходов СМИ, которая бы решала какую-либо задачу из следующих возможных:
- обеспечить заданную величину какого-либо медиапараметра (например, эффективного охвата аудитории, доли голоса) при минимальном рекламном бюджете,
- достичь максимального значения какого-либо параметра (эффективного охвата, доли голоса) при заданном бюджете.
После того, как выбран количественный критерий эффективности размещения рекламы, можно приступать к оптимизации медиаплана. Оптимизация может быть организована либо с помощью анализа охватов аудитории, осуществляемой в рамках имеющейся базы данных, либо с помощью аналитического прогнозирования в рамках математической модели, использующей данные измерений. Заметим, что если используется вторая возможность, то удаётся обойтись значительно меньшим числом данных измерений. Применение математических моделей позволяет, с одной стороны, использовать меньше исследовательских данных, с другой — достигать результатов, которые нельзя получить с помощью подходов, основанных на использовании только данных измерений. В частности, это относится к информации об охватах пересечений разных СМИ. Получить при помощи опросов достоверную и полную информацию об охватах всех пересечений СМИ, используемых при оптимизации, практически невозможно из-за большого объёма и стоимости соответствующих исследований (ниже мы рассмотрим в этой связи необходимые объёмы выборки).
Ошибки измерения медиапараметров
В данном разделе рассмотрим вопросы, связанные с достоверностью измерений рейтингов медиа. Точность измерения рейтингов являются определяющей для точности процедуры оптимизации медиаплана.
Из теории выборочного метода известно соотношение для ошибки измерения Δ рейтинга в зависимости от объёма выборки n и величины рейтинга R: Δ = t [R (1 – R)/n ]1/2. (1). Коэффициент t в формуле (1) определяется по заданному уровню надёжности γ с помощью функции Лапласа. Например, уровню надёжности γ = 95% соответствует значение t= 1,96, а уровню надёжности γ = 99% соответствует t =2,576. Отметим, что формула (1) справедлива для случая, когда объём исследуемой совокупности существенно превышает объём выборки. Это условие практически всегда выполняется при исследовании медиапредпочтений населения.
В таблице 1 представлены данные о зависимости ошибки измерения Δ от объема выборки n для разных значений рейтинга R .
Таблица 1
Ошибка измерения Δ в зависимости от рейтинга R и объема выборкиn (γ = 95%)
|
n
|
70
|
100
|
200
|
500
|
1000
|
|
R,%
|
|
значения
|
Δ,%
|
|
|
|
5
|
5
|
4
|
3
|
2
|
1,4
|
|
10
|
7
|
6
|
4
|
2,6
|
2
|
|
20
|
9
|
8
|
5,5
|
3,5
|
2,5
|
|
50
|
12
|
10
|
7
|
4
|
3
|
Проанализируем ошибки некоторых рейтингов из таблицы 1. Возьмём рейтинг R =5%. Если он получен по выборке n = 1000, то ошибка его измерения составляет Δ= 1,4%. Если же этот рейтинг получен по выборке n = 70, то ошибка его измерения Δ=5%. То есть рейтингR =5% при выборке n = 70 является недостоверным, поскольку ошибка его измерения равна величине самого рейтинга. Из этого примера понятно, что при определении рейтинга целевых групп объём выборки должен быть таким, чтобы ошибка измерения не превосходила величину рейтинга, иначе рейтинги будут недостоверны.
Назовем рейтинг, равный ошибке измерения, минимально значимым рейтингом и обозначим его символом Rmin. Смысл Rmin заключается в том, что его величина указывает на границу, опускаясь ниже которой, рейтинги при заданном объёме выборки становятся недостоверными, поскольку ошибка их измерения начинает превышать саму измеряемую величину. Используя выражение (1), можно получить следующую формулу для минимально значимого рейтинга Rmin: Rmin = t2/(n + t2) (2).
В таблице 2 приведены зависимости минимально значимых рейтингов от объёма выборки, вычисленные по формуле (2) для уровня надёжности γ = 95%, [19].
Таблица 2.
Минимально значимый рейтинг Rmin в зависимости от объёма выборки n.
| Rmin, % |
n
|
|
0,1
|
3838
|
|
0,3
|
1277
|
|
0,5
|
764
|
|
0,7
|
545
|
|
1
|
380
|
|
2
|
188
|
|
4
|
92
|
|
6
|
60
|
|
8
|
44
|
|
10
|
35
|
Проанализируем данные, представленные в таблице 2. С уменьшением объёма выборки происходит резкоеснижение точности измерениярейтингов. Так, при объеме выборки n= 380 человек недостоверны рейтинги меньше 1%, при n= 60 недостоверны рейтинги меньше 6%.
Теперь рассмотрим проблему точности медиаизмерений с точки зрения медиапланирования. Для корректной оптимизации медиапланов необходимо знать как охваты отдельных СМИ, так и охваты совместного воздействия (пересечения) двух, трёх и большего числа СМИ. Получить базу, в которой содержалась бы информация обовсех пересечениях СМИ — задача практически неосуществимая. Допустим, что мы решили упростить задачу и учесть пересечения только пар и троек СМИ. При этом нужно помнить, что уже это упрощение делает результаты оптимизации, полученные по таким данным, лишь приближёнными. Тем не менее, оценим объёмы выборки, которые позволят измерить охваты пересечений СМИ с достаточной точностью. Охваты тройных пересечений СМИ с рейтингом ~10% имеют порядок 0,1%. Согласно табл. 2, объём выборки, нужный, чтобы минимально значимый охват был равен 0,1%, составляет 3838 респондентов (при уровне надёжности γ = 95%). Из этого примера следует, что точная информация об охватах пересечений СМИ является практически недоступной, поскольку для её получения требуются выборки большого объёма.
Приведенные выше оценки показывают, что невозможно осуществить точную оптимизацию с использованием только данных измерений. Однако охваты пересечений СМИ можно определить не только по базе измерений, но и путём вычислений, которые основаны на методах теории вероятностей, математической статистики и теории оптимизации.
Из данных, приведённых в таблицах 1 и 2, следует, что объёмы выборки в 500–1000 человек вполне достаточны для надёжного измерения рейтинга. При этих объёмах минимально значимый рейтинг заключён в пределах 0,4%-0,8%, а максимальная ошибка измерения – в пределах 3%-4%, что вполне приемлемо. Охваты же пересечённых областей вычисляются с помощью теории, в которой в качестве входных данных используются рейтинги и предельные охваты СМИ, найденные с помощью измерений. При этом для получения информации о пересечённых областях не нужныбольшие объёмы выборки, которые требуются в случае применения чисто измерительных подходов.
Основы количественной теории медиапланирования
Математически теория медиапланирования основана на теории вычислениячастотного распределения охвата. В рамках данной статьи подробное изложение всех вопросов теории не представляется возможным. Тем не менее, далее будут изложены основные положения теории, которые могут быть использованы на практике при планировании рекламных кампаний.
Вначале остановимся на методах вычисления охвата аудитории любого СМИ. Для того, чтобы рассчитать охват аудитории в зависимости от числа выходов данного СМИ (это число выходов обозначим символом m), а также в зависимости от любого возможного числа контактов fс этим СМИ, нужно знать только два параметра: рейтинг R и предельный охватG∞ данного СМИ. Для краткости записи формул мы используем для охвата обозначение G вместо общепринятого Reach. Данные о R иG∞ получают в результате медиаисследований. Если известны R иG∞, то охват g(f), соответствующий числу контактовf, вычисляется по формуле g(f) = G∞ (R/G∞)f (1 – R/G∞)m-f (4), где m – число выходов СМИ, (R/G∞)f (1 – R/G∞)m-f (4), где m – число выходов СМИ,  = m!/f!/(m– f)! — биномиальные коэффициенты. Функцию g(f) называют частотным распределением охвата, или распределением охвата по частоте контактов, или спектром охвата. Знание спектра охвата даёт полную информацию о СМИ с точки зрения его коммуникационных возможностей, поскольку, знаяg(f), можно вычислить все наиболее важные количественные характеристики медиа – полный и эффективный охваты, эффективное число контактов, среднее эффективное число контактов, долю голоса. = m!/f!/(m– f)! — биномиальные коэффициенты. Функцию g(f) называют частотным распределением охвата, или распределением охвата по частоте контактов, или спектром охвата. Знание спектра охвата даёт полную информацию о СМИ с точки зрения его коммуникационных возможностей, поскольку, знаяg(f), можно вычислить все наиболее важные количественные характеристики медиа – полный и эффективный охваты, эффективное число контактов, среднее эффективное число контактов, долю голоса.
Пример 1. Пусть СМИ с рейтингом R= 8% и предельным охватом G∞ = 24% вышло четыре раза. Какой процент целевой аудитории будет иметь с этим СМИ: 1) один контакт, 2) два контакта, 3) три контакта, 4) четыре контакта?
Решение. Используя формулу (4) при m = 4, получим:
1) g(1) = 0,24 * 4 * (0,08/0,24)1 * (1– 0,08/0,24)3 = 9,5%;
2) g(2) = 0,24 * 6 * (0,08/0,24)2 * (1 – 0,08/0,24)2 = 7,1%;
3) g(3) = 0,24 * 4 * (0,08/0,24)3 * (1 - 0,08/0,24)1 = 2,4%;
4) g(4) = 0,24 * (0,08/0,24)4 = 0,3%.
Полный охват СМИ, по определению, равен сумме охватов, соответствующих всем возможным числам (частотам) контактов (5). Нетрудно показать, что из формул (5) и (4) вытекает простая формула для вычисления полного охвата одного СМИ G =G∞ [1 – (1 – R /G∞)m ] (6).
 (5) (5)
Пример 2. Найти охват пяти выходов СМИ с рейтингом R= 8% и предельным охватом G∞ = 24%.
Решение. Подставляя данные из условия задачи в формулу (6), получим:
G = G∞ [1 – ( 1 – R/G∞)m ] = 0,24* [1 – (1 – 0,08/0,24)4] = 19,3%.
Проверка. Используя формулу (5) и результаты предыдущей задачи, находим G = 9,5%+ 7,1%+ 2,4%+ 0,3%= 19,3%. Таким образом, охват СМИ, найденный двумя разными способами, равен одной и той же величине, и вычислен правильно.
Теперь приведём формулу для вычисления охвата нескольких СМИ. Полный охват нескольких СМИ вычисляется формулой (7) , где G∞ — предельный охват группы СМИ; Gj — охват отдельного СМИ с номером j, который вычисляется по формуле (6); Π — знак произведения. Если обращения к СМИ имеют случайный характер, то вместо формулы (7), можно использовать более простую формулу (8), которая следует из (7) 1 – Gj) (8).
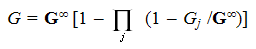 (7) (7)
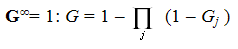 (8) (8)
Общая формула для спектра охвата нескольких СМИ приведена в работе [20]. Поскольку она довольно громоздкая, мы её здесь не приводим.
Пример 3. Записать формулы для охватов двух, трёх и четырёх СМИ.
Решение. В литературе для охватов СМИ иногда используются следующие обозначения: А, B, C, D (например, [1], с. 256, [10], с. 44, [13], с. 80). При решении данной задачи для удобства сопоставления наших формул с приведёнными в литературе будем использовать эти же обозначения: G1 = А; G2 = B; G3 = C; G4 = D.
Подставив в формулу (8) новые обозначения для охватов СМИ и раскрыв скобки, найдем формулы для полных охватов двух, трёх и четырёх СМИ.
а) Охват 2 СМИ G = 1 – (1 – А) (1 – B) = A + B – AB.
б) Охват 3 СМИ G = 1 – (1 – А) (1 – B) (1 – C) = A + B+ C – AB – BC – AC + ABC.
в) Охват 4 СМИ G =1 – (1 – А) (1 – B) (1 – C) (1 – D) = A + B + C + D – AB– AC – AD – BC – BD – CD + ABC + ABD+ ACD + BCD– ABCD.
Из этого примера видно, что общая формула (8) гораздо удобнее, чем формула, полученная после раскрытия скобок. Подставив конкретные значения охватов СМИ, можно убедиться в том, что результаты вычислений по данным формулам (до и после раскрытия скобок) одинаковы. Например, при А=10%, В=15%, С=20% и D=25% по обеим формулам получим G= 54,1%. К сожалению, в литературе эти формулы часто записывают с ошибками (например, [10], с. 44, [13], с. 80).
Знание спектра охвата позволяет вычислять эффективный охват — долю людей целевой аудитории с числом контактов, не меньшем уровня эффективной частоты fэф (см. формулу (9)).
 (9) (9)
Практическая значимость эффективного охвата заключается в том, что при оптимизации он позволяет исключить из рассмотрения людей, число контактов которых меньше эффективной частоты fэф.
Пример 4. Найти охват c числом контактов 2 и более G(2+) в условиях примера 2.
Решение. Используя формулу (9) и результаты примера 1, находим G(2+) = g(2) + g(3) + g(4) = 7,1%+ 2,4%+0,3% = 9,8%.
Таким образом, эффективный охват составил всего 9,8%, что почти в 2 раза меньше, чем полный охват (19,3%, см. пример 2).
В заключение этого краткого обзора теории приведём ещё несколько формул, позволяющих вычислять эффективное число контактов по целевой группе (суммарный рейтинг, TRP) и среднее число (частоту) контактов fcp , приходящихся на одного человека из охваченной аудитории (см. формулы (10), (11))
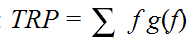 (10) (10)
fcp = TRP/G (11).
Смысл этих характеристик рекламной кампании очень прост: TRP — это число контактов со СМИ, выраженное в процентах от численности N целевой аудитории. Умножив TRP на N, получим полное число контактов. Если умножить числитель и знаменатель правой части равенства (11) на N, то получим среднее число контактов как частное от деления числа всех контактов на число всех охваченных людей.
Для оптимизации рекламного бюджета нужно подбирать такие выходы рекламы, которые бы максимизировали эффективный охват, вычисляемый по формуле (9) при заданном рекламном бюджете или минимизировали рекламный бюджет, обеспечивающий достижение заданного уровня охвата.
Выводы
На основе теории медиапланирования можно создать различные варианты компьютерных программ по медиапланированию (например [19], [21]). Эти программы позволяют самостоятельно планировать мультимедийные рекламные кампании, используя такие критерии оптимизации, как оптимизация по мультимедийному эффективному охвату Reach(n+), по доле голоса (Share Оf Voice), по прогнозируемым продажам и прибыли от рекламы с учётом дисконтированных денежных потоков [22], вычислять период рекламной кампании в зависимости от уровня её интенсивности [24]. В результате определяются оптимальные выходы рекламы и оптимальные рекламные бюджеты.
Таким образом, теория медиапланирования дает возможность менеджерам по рекламе самостоятельно оптимизировать размещение рекламы, вычислять и прогнозировать её основные количественные характеристикина основе минимального набора данных медиаисследований. Значение оптимизации размещения заключается в том, что «неэффективный график размещения рекламы может сделать эффективную рекламу совершенно неэффективной» ( [6], с.34). Перечислим основные возможности количественной теории медиапланирования:
· Вычисление всех медиапараметров рекламной кампании (фактического и эффективного охватов, их частотных распределений,долей голоса на основе данных о рейтингах, предельных охватах и параметрах эффективности контактов).
- Оптимизация периода рекламной кампании в зависимости от уровня её интенсивности.
- Оптимизация размещения и бюджета мультимедийной рекламы.
- Явный количественный учёт влияния рекламы конкурентов на эффективность рекламы.
- Планирование рекламы с учётом синергетического эффекта при наличии СМИ разных типов.
- Прогнозирование продажиприбыли, обусловленных рекламой.
- Количественная оценка коммуникационной и экономической эффективности рекламы
- Доступность в использовании, в том числе невысокая стоимость программных продуктов.
ЛИТЕРАТУРА
- Сиссорс Дж. З., Бэрон Р. Е. Рекламное медиапланирование. - СПб.: Питер, 2004.
- Хопкинс К. Реклама: Научный подход.- М.: Альфа-Пресс, 2000.
- Сэндидж Ч., В. Фрайбургер, К. Ротцолл.Реклама: теория и практика. - М.: Сирин, 2001.
- Росситер Дж. Р., Перси Л. Реклама и продвижение товаров. - СПб.: Питер, 2000.
- Батра Р., Майерс Дж., Аакер Д. Рекламный менеджмент. - СПб, Вильямс, 1999.
- Дю Плесси, Э.. Психология рекламного влияния. - СПб.: Питер, 2007.
- Рекламный бизнес / Под ред. Дж. Ф. Джоунса. - М.: Вильямс, 2005.
- Rust R. Advertising Media Models: A Practical Guide. Lexington, MA: Lexington Books, 1986.
- Dayer R. F., Forman E. H., Musstafa M. A. Decision Support for Media Selection Using the
- Analytic Hierarchy Process // J. of Advertising. 1992. V. 21, nr 1. P. 59—72.
- Балабанов А. В. Занимательное медиапланирование. - М.: РИП-холдинг, 2001.
- Назайкин А. Н. Медиапланирование на 100 %. - М.: Альпина Бизнес Букс, 2007.
- Бузин В. Н., Бузина Т. С. Медиапланирование для практиков. - М.: Вершина, 2006.
- Кочеткова А. В. Медиапланирование: социологические и экономические аспекты - М.: РИП-холдинг, 2005.
- Кокрен У. Методы выборочного исследования. М.: Статистика, 1976.
- Математические методы анализа и интерпретации социологических данных. М.: Наука, 1989.
- Паниотто В. И., Максименко В. С. Количественные методы в социологических исследованиях. Киев: Наук. думка, 1982.
- Данько Т.П., Косоруков О.А. и др.Количественные методы анализа в маркетинге. СПб.: Питер, 2005.
- Мищенко А.В., Джамай Е.В. Динамическая задача определения оптимальной производственной программы // Менеджмент в России и за рубежом. - 2005. - № 3.
- Власов М.В., Попов Е.В. Оптимизация процесса управления новыми знаниями// Менеджмент в России и за рубежом. - 2007. - № 4, с.4-6.
- Шматов Г. А. Основы медиапланирования: эвристический подход. - Екатеринбург: УрГУ, 2005. - 332 c.; 2 изд. – 2007 г., 376 с.
- Шматов Г. А. Математические основы медиапланирования // Деп. ВИНИТИ 04.06.03, № 1090–В2003. - Екатеринбург: УрГУ - 108 с.
- Рязанов Ю. Г., Шматов Г. А. Медиапланирование. - Екатеринбург: Уральский рабочий, 2002. - 308 с.
- Шматов Г. А. Оценка эффективности рекламы методом дисконтированных денежных потоков // Маркетинг и маркетинговые исследования в России. - 2005. - № 3, с 79-86.
- Шматов Г. А. Медиапланирование: новый подход // Реклама. Теория и практика. – 2006. - № 1, с. 10-23.
- Шматов Г. А. Оптимизация периода размещения рекламы//Реклама: теория и практика. - 2008. - № 1, с. 24-31.
|


 (9)
(9)