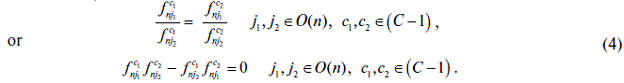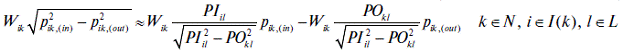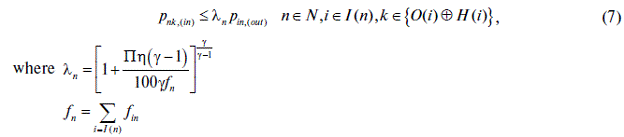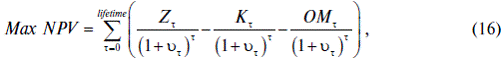|
Doví M-S.,
Yenching Academy,
University of Peking,
Beijing, China
Meshalkin V.P.,
academician of the Russian
Academy of Sciences, head
of the department logistics and economic
to an informatikirkht of D.I. Mendeleyev,
chief research scientist IONH
Russian Academy of Sciences of N.S. Kurnakov
Kantiukov R.R.,
Dmitry Mendeleev
University of Chemical Technology
of Russia
While the economic optimization problem of the structure design and operation management of natural gastransportation networks (NGTN) has been the object of a large amount of research work in economics, manegement organization, logistics and supply chain managementthe large computational costs presently available makes it possible to include additional issues capable of effectively formulating and implementing increasingly complex and robust mathematical models and algorithms.
In this article, the possible delivery of natural gas (NG) and liquid natural gas (LNG) at multiple feed-in points is added to the most general mathematical models, with use of mixed integer linear programming (MILP), whereas the further inclusion of financialand environmental constraints. The goal of this article is double: classification and System analysis of the most general mathematical models and algorithms, capable of providing a complete decision support tool, and to show how simplified mathematicalmodels can be obtained from them if the complexity of the gas transportation network makes it necessary to reduce the computational load.
Keywords: natural gas, supply chain management, energy efficiency, mathematical modeling and optimization, mixed linear integer programming.
There is a vast amount of literature on natural gas (NG) transportation networks (NGTN) optimization. This is partly due to the fact that several different disciplines are involved in this field, such as chemical engineering, management, energy economics, logistics, environmental sciences and operations research.
This variety of approaches has led to the development of partial specific models in the different areas of interest, according to the perspective of each scientific area.
While technical models for structure design and operation management of upstream and downstream infrastructure have been developed and implemented by chemical engineers, logisticians, managers and market mechanisms modeling have been generally elaborated by operations research scientists, energy and ecological economists. Environmental concerns have recently given rise to a rapid growth of publications in green and sustainable supply chain models of natural gas production, transportation and distribution.
One of the first technical models concerning production planning in NGTN dates back to 1960 years [1], followed by more and more sophisticated algorithms employed for the solution of increasingly complex descriptions of technical NGTN structures. Thus, for example, one of the first algorithms based on successive quadratic programming for optimizing NGTN was presented by Fury [2]. Later developments included NGTN design optimization by De Wolf and Smeers using a bundle method [3] and piecewise linearization combined with linear programming [4]. A Lagrangean algorithm for the solution of the resulting optimization problem has been proposed by Van den Heever et al. [5]. Mixed integer linear programming (MILP) algorithms have been proposed in several articles. Among them, Ortíz-Gómez et al. [6], Möller [7], and Martin et al. [8]. A very general simulation model for NGTN is presented by Nimmanonda et al. [9], while Barragán-Hernández et al. [10] propose an algorithm for the simultaneous optimization of oil and gas production.
Optimization under uncertainty (limited to the production phase) has been introduced by Goel et al. [11], whereas nonlinear programming algorithms have been employed by Kabirian and Hemmati [12] for the structure design of NGTN. Non-linear models have been generalized by Wu et al. [13] to the non-convex case of a NGTN optimization using Floudas’ Global optimization algorithm [14]. Recent articles by Osiadacz [15] and Osiadacz and Chaczykowski [16] provide algorithms for optimal control under steady state and transient conditions.
The inclusion of cost analysis into both the objective function and the constraints that constitute the general optimization task grew out of their increasing importance in shaping gas production, transportation, and delivery.
Jonsbråten [17] considered the optimization of the production in oil fields, whereas Chermak et al. [18] extended the model to natural gas production.
The article is organized as follows. In the next section, the general model will be developed and suitable optimization tasks will be analyzed. In the following section, the resulting numerical algorithms will be examined in terms of convergence properties and of computational load.
In the Conclusions, potential applications and the consequences for real cases will be considered.
General mathematical models
As anticipated, we have taken into accountthe incorporation of LNG system at multiple feed-in points of the overall gas transportationusing one of the most general mathematical models, (i.e. the one suggested by Tomasgard et al. [19]), without considering the optimization of financial portfolios and the presence of methane fugitive leaks in the greenhouse gases (GHG) balance of natural gas supply chains. Both issues will be examined in a future article.
Mathematical models structure, the physical and chemical constraints The following set ofmathematical model equations and specific constraints are related to conditions due to physical and chemical factors.
(i) Multicomponent mass balance equations including NG or LNG transport We follow the symbols proposed by Tomasgard et al. [19] as reported in the Notation section and provide new symbols for the variables not accounted for by them. Additional symbols are introduced and explained directly in the text.
The total mass balances at each element or fisical and technical node of NGTN, which can be reprezanted as a direction graph can be expressed as

Total mass balances are not sufficient if gas quality and multi-component flows are to be taken into account. The conditions on gas quality and composition at the delivery nodes make it necessary to keep track of the quality in every node of the GTN.
The quality is generally expressed as:

The compositions of flow rates are subject to two types of equations or constraints:
- (C-1) mass balances for the species present (the C-th is contained in the total mass balance).
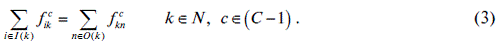
- composition uniformity of different flow rates going out of the same node (pooling condition).
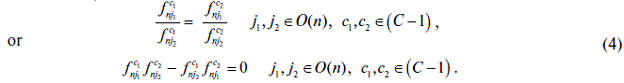
Both sets of equations or constraints (2) and (4) are nonconvex, quadratic constraints.
The presence of this type of constraints makes both convergence and computational load of the resulting optimization problem much more onerous. Indeed it has been proven that the problem is NP-hard [20].
Various algorithms have been proposed for decision this problem, either using non linear programming techniques or by introducing discretizations and suitable variable transformations, with a view to remodeling the constraints into a set of linear equations containing integer variables.
The presence of integer variables is precisely the price for reducing the quadratic constraints to a linear form. Different linearization techniques (all leading to MILP problems) have been recommended in the literature. We can use the approach proposed by Kolodziej et al. [21], i.e. given the quadratic term  , we can rewrite it in a mixed integer linear form as follows: , we can rewrite it in a mixed integer linear form as follows:

where P must be large enough for  to be at least as large as the upper bound on to be at least as large as the upper bound on  , i.e. , i.e.  and p small enough for the range p + 1, …, P – 1 to contain at least one (but preferably many) discretization points. and p small enough for the range p + 1, …, P – 1 to contain at least one (but preferably many) discretization points.
(ii) Momentum balance equations and pressure drops and surges In long pipelines of NGTN there can be substantial pressure drops (for instance in offshore transportation or in any section of a network system without compression). Generally, pressures at production sites (including NG or LNG regassifying stations) are specified (even if some flexibility is frequently foreseen). Furthermore pressures at delivery stations is frequently regulated by contractual agreements. Thus, it is necessary to take into account pressures in the pipeline system.
The Weymouth equation is frequently used to establish a relationship between flows and differences in input and output pressure. In particular, the flow from node i to node j can be expressed as a function of the pressure difference between the two nodes as follows:

where  is the Weymouth constant, which depends on length and physical-chemical properties of both pipeline and gas. is the Weymouth constant, which depends on length and physical-chemical properties of both pipeline and gas.
This relation can be linearized [22] by considering a range of values for  and and 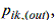  around which the Weymouth equation is linearized in the form ( around which the Weymouth equation is linearized in the form ( order Taylor’s expansion): order Taylor’s expansion):
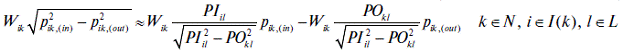
For all values of  the following relations hold true the following relations hold true

Only one of these L constraints is binding, i.e. the one that approximates the flow best.
Obviously, if pressure drops are negligible, equations (5) are replaced by

Nodes of NGTN with / without compression
Unless there is a compression at node n, the input pressure of all arcs going out of n must be lower than the lowest pressure for any arc going into node n, i.e.

However, if the flow in a pipeline into node n is zero (i.e. if the optimal solution has to allow for a pipeline to be shut down), the latter constraint can be cast into the form:

where  is a large positive number. If the flow is a large positive number. If the flow 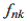 is zero, is zero, 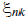 s set to zero and the constraint on pressure is not active. If both s set to zero and the constraint on pressure is not active. If both 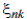 and and 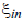 are equal to 1, the constraint on the flow is not active , while the constraint on the pressures is equal to the previous constraint. are equal to 1, the constraint on the flow is not active , while the constraint on the pressures is equal to the previous constraint.
Thus, the possibility of any flow to be zero is automatically taken into account by this notation without any need of explicitly requiring any arc of pipeline to be shut down.
If there is indeed a compression, the relation between pressures out of node n and pressures into node n are related by the inequality:
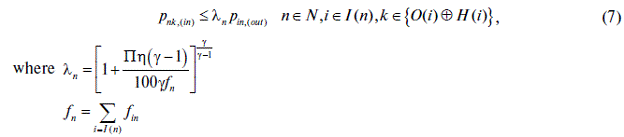
and  is the power output of the compressor, is the power output of the compressor,  its efficiency and its efficiency and  is the adiabatic constant of the gas mixture. is the adiabatic constant of the gas mixture.
(iii) Production, Demand and Processing limitations
Production capacity
An obvious constraint limits the total flow out of a production node in NGTN g to the maximum planned production in that node.

where g indicates a production field.
Demand
Constraints on demand limit the total flow into a node with customers to the demand of that node:

Gas processing plants
Some components of the NG of LNG can be extracted and moved out of the network system.
The amount of each component extracted is assumed to be proportional to the total amount of that component flowing into the processing node.
This model can be accounted for through the introduction of the additional constraints:

The set of constraint (1)…(11) makes it possible to evaluate the variables contained in them, provided suitable economical objective functions are optimized.
Three main limitations have implicitlybeen considered so far:
1) the network system is under stationary conditions
2) financial aspects are not part of the optimization task (economic assessment can indeed be included in the objective function, but no financial transaction involving spot and futures prices is allowed for)
3) environmental concerns are not included
The first limitation will be eliminated when introducing storage fluctuations in a section below, whereas eliminating the last two limitations is the goal of a future publication. Indeed, simplifications and reductions to sub-models can be computationally convenient while maintaining a high degree of reliability whenever some issues prevail largely over those that in particular cases can be neglected.
Within these restrictions, two classes of optimization problems can be considered:
- problem № 1 – evaluation of optimal operation management conditions;
- problem № 2 – optimal structure design of NGTN.
Problem N.1
An economical objective function as operation profit Z:

where
 unitary volume price for gas delivery at node m unitary volume price for gas delivery at node m
 proportionality factor for the cost of energy necessary to the transport of gas proportionality factor for the cost of energy necessary to the transport of gas
 penalty cost for underproduction or overproduction with respect to the planned penalty cost for underproduction or overproduction with respect to the planned
production at node g
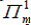 penalty cost for deviation from contracted pressures at delivery nodes penalty cost for deviation from contracted pressures at delivery nodes
 penalty cost for deviation from contracted quality levels at delivery nodes penalty cost for deviation from contracted quality levels at delivery nodes
The maximization of profit Z (12) has to be carried out subject to the constraints (1)- …- (11).
Either (5) or (5’) is to be used depending on the presence of pressure drops.
Indicating positive and negative deviations with the (+) and (-) superscripts, we can rewrite
 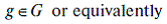

If the penalty costs are proportional to the deviations, the objective function (12) can be rewritten as

where  are the cost coefficients of the deviations from planned or contracted values. are the cost coefficients of the deviations from planned or contracted values.
Problem N.2
An objective function – the Net Present Value (NPV):
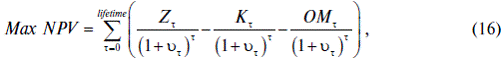
where
 is the capital cost incurred in year is the capital cost incurred in year 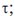
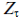 is the term described by equation (12’) for each year is the term described by equation (12’) for each year 
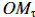 is the cost for operation and maintenance in year is the cost for operation and maintenance in year 
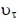 is the opportunity interest rate in year is the opportunity interest rate in year 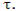
The objective function – NPV (16) is to be maximized subject to the same constraints as problem № 1.
(iv) Storage limitations
Both the presence of a fluctuating gas demand (especially as a consequence of seasonal demand patterns) and the possibility of exploiting the advantages offered by the liberalization of the natural gas industry for financial operations underscore the strategic role of gas storages and increase the flexibility of decisions related to production and transportation in the network system at the price of introducing time dependence.
Storages include abandoned oil- and gas reservoirs, aquifers, caverns and aboveground NG or LNG-storages.
Additional constraints are provided by the changing levels of storages and by the maximum values of both inflow and outflow rates being limited by the current levels of the storages.
While the maximal inflow rate is a decreasing function of the level, the outflow rate is given by an increasing function of the level. The nonlinear character can be modelled using special ordered sets of type 2 (SOS2 or S2) which are an ordered set of non-negative variables, of which at most two can be non-zero, and if two are non-zero these must be consecutive in their ordering.
To this purpose suppose the storage levels are discretized by s values  which correspond to maximal inflow and outflow rates which correspond to maximal inflow and outflow rates  respectively. At intermediate levels the maximal flowrates are provided by linear interpolation. The maximal flowrates can therefore be represented by respectively. At intermediate levels the maximal flowrates are provided by linear interpolation. The maximal flowrates can therefore be represented by

and consequently the constraints on maximal flowrates can be cast into the form:

The constraint on  being a SOS2 can be satisfied setting the conditions: being a SOS2 can be satisfied setting the conditions:

and introducing the additional set of variables  such that: such that:

The time-dependent mass balances are given by

where  indicates the level of storage s at time t. indicates the level of storage s at time t.
Problem N.3
An optimization problem capable of accounting for the GTN structure flexibility introduced by the presence of storages must allow for the variables contained in eq. 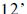 (or in eq. 16) to be time dependent over the seasonal variability and consider, in addition to the new constraints (17)-…-(22), an objective function that extends over all seasonal periods, such as (or in eq. 16) to be time dependent over the seasonal variability and consider, in addition to the new constraints (17)-…-(22), an objective function that extends over all seasonal periods, such as

or

While the objective functions  and and  take into account seasonal variability, the NGTN structure and mode flexibility introduced by storages in commodities trading and market transactions will be examined in a future publication. take into account seasonal variability, the NGTN structure and mode flexibility introduced by storages in commodities trading and market transactions will be examined in a future publication.
Numerical algorithms and programm compelexes
The structure of both objective functions 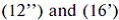 and constraints, as well as the techniques described for dealing with non-linearities (such as the use of special ordered sets (SOS) of type 1 and 2 (SOS1, SOS2) make it possible to cast the optimization problems (12), (16) and and constraints, as well as the techniques described for dealing with non-linearities (such as the use of special ordered sets (SOS) of type 1 and 2 (SOS1, SOS2) make it possible to cast the optimization problems (12), (16) and  into a linear form. However, all but the most elementary mathematical models include integer variables. The presence of integers are related to the necessity of considering gas concentrations, storage levels and other linearly discretized functions. Consequently the problems type 1, 2 and 3 correspond to reliable and readily available mixed-integer linear programming (MILP). into a linear form. However, all but the most elementary mathematical models include integer variables. The presence of integers are related to the necessity of considering gas concentrations, storage levels and other linearly discretized functions. Consequently the problems type 1, 2 and 3 correspond to reliable and readily available mixed-integer linear programming (MILP).
In addition to the well known and highly efficient code CPLEX (contained in GAMS, [23]), public domain codes, such as GUSEK [24], provide powerful tools for solving real NGTN problems based on the models described in the previous section.
When the size of the problem is limited, linearizations can be avoided and non linear mixed-integer techniques can be tried (GAMS, [23]). However, it should be remembered that the non convexity of the original (non-linearized) mathematical model does not guarantee the attainment of the global optimum, but only convergence to a local solution. Furthermore, even local convergence may fail to occur.
Commercial software for general supply chains have been on the market for some time.
Thus, Funaki [26] provides an overview of the 13 most important products. On the other hand, available commercial software for NGTN is generally proprietary and not available for general use.
Conclusions
The review of existing models of natural gas networks and the introduction of some new issueshave shown the wide range of problems that natural gas networks optimization can successfully solve.
However, the more accurate the modelling and the more issues are accounted for, the more onerous the computational burden will be. While comparatively small, regional networks (such as the one considered by Kantyukov, Popov et al., [27]) can and will be analyzed using the full power of the algorithms previously described, the computational effort for large systems may turn prohibitive. Indeed, MILP problems (to which all models can be reduced) are extremely computing intensive.It is therefore sometimes necessary to reduce the number of effects and/or issues to be analyzed.
Similarly, arcs and nodes can be grouped together with a view to reducing the size of the problem and approximate, sub-optimal solutions can be obtained in a reasonable computational time after some conditions are relaxed. For instance, time-dependent solutions can be too time-consuming for large systems, steady-state conditions should be considered instead. Design and operation optimization problems can be solved separately, with an obvious reduction of the computational effort.
Tomasgard et al. [19] suggests interrupting the branch&bound method used for solving MILP problems when the integer variables have an integrality gap of 5%.
In other words, the algorithm adopted depends largely on the focus of the analysis. There is not yet an off-the-shelf algorithm. Technical expertise, numerical skill and ecomic insight are still required for large gas network systems to be correctly formulated and successfully solved.
Notation

References
1. Van Dam J. Planning of optimum production from a natural gas field // Journal of the Institute of Petroleum. 1968. Vol. 54. pp. 55–67.
2. Furey B.P. A sequential quadratic programming-based algorithm for optimization of gas networks // Automatica. 1993, Vol. 29. pp. 1439–1450.
3. De Wolf D., Smeers Y. Optimal dimensioning of pipe networks with application to gas transmission networks // Operations Research. 1996. Vol. 44, pp. 596–608.
4. De Wolf D., Smeers Y. The gas transmission problem solved by an extension of the simplex algorithm // Management Science. 2000. 46. 1454–1465.
5. Van den Heever S.A., Grossmann I.E., Vasantharajan S., Edwards K. A Lagrangean decomposition heuristic for the design and planning of offshore hydrocarbon field infrastructures // Industrial and Engineering Chemistry Research. 2001. Vol. 40. pp. 2857–2875.
6. Ortíz-Gómez A., Rico-Ramirez V., Hernández-Castro S. Mixed-integer multiperiod model for the planning of oilfield production // Computers and Chemical Engineering. 2002. Vol. 26, pp. 703–714.
7. Möller M. Mixed Integer Models for the Optimisation of Gas Networks in the Stationary Case. PhD thesis. 2004, TU Darmstadt. URL: http: //tuprints.ulb.tu-darmstadt.de/438/
8. Martin A., Möller M., Moritz S. Mixed integer models for the stationary case of gas network optimization // Mathematical Programming. 2006. Vol. 105. pp. 563–582.
9. Nimmanonda P., Uraikul V., Chan C.W. and Tontiwachwuthikul P. Computer-aided simulation model for natural gas pipeline network system operations // Industrial and Engineering Chemistry Research. 2004. Vol. 43. pp. 990–1002.
10. Barragán-Hernández V., Vázquez-Román R., Rosales-Marines L., García-Sánchez F. A strategy for simulation and optimization of gas and oil production // Computers and Chemical Engineering. 2005. Vol. 30. pp. 215–227.
11. Goel V., Grossmann I.E., El-Bakry A.S., Mulkay E.L. A novel branch and bound algorithm for optimal development of gas fields under uncertainty in reserves // Computers and Chemical Engineering. 2006. Vol. 30. pp. 1076–1092.
12. Kabirian A., Reza Hemmati M. A strategic planning model for natural gas transmission networks // Energy Policy. 2007. Vol. 35. pp. 5656–5670.
13. WuY., Lai K.K., LiuY. Deterministic global optimization approach to steady-state distribution gas pipeline networks // Optimization and Engineering. 2007. Vol. 8. pp. 259–275.
14. Floudas C.A., Aggarwal A., Ciric A.R. Global optimum search for nonconvex NLP and MINLP problems // Computers and Chemical Engineering. 1989. Vol. 13. pp. 1117–1132.
15. Osiadacz A.J. Steady State Optimisation of Gas Networks // Arch. Min. Sci. 2011. Vol. 56. pp. 335–352.
16. Osiadacz A.J., Chaczykowski M. Dynamic Control for Gas Pipeline Systems // Arch. Min. Sci. 2016. Vol. 61. pp. 69–82.
17. Jonsbråten T.W. Oil field optimization under price uncertainty // Journal of the Operational Research Society. 1998. Vol. 49. pp. 811–818.
18. Chermak J.M., Crafton J., Norquist S.M., Patrick R.H. A hybrid economic-engineering model for natural gas production // Energy Economics. 1999. Vol. 21. pp. 67–94.
19. Tomasgard A., Rømo F., Fodstad M., Midthun K.T. Optimization models for the natural gas value chain. 2007. Technical report, Norwegian University of Science.
20. Alfaki M., Haugland D. Strong formulations for the pooling problem.// Journal of Global Optimization. 2013. Vol. 56. pp. 897–916.
21. Kolodziej S., Castro P.M., Grossmann I.E. Global optimization of bilinear programs with a multiparametric disaggregation technique // Journal of Global Optimization. 2013, Vol. 57, pp. 1039–1063.
22. Midthun K.T., Mette B., Tomasgard A. Modeling Optimal Economic Dispatch and System Effects in Natural Gas Networks // The Energy Journal. 2009. Vol. 30. pp. 155-180
23. McCarl B.A., Meeraus A., van der Eijk P., Bussieck M., Dirkse S., Nelissen F. McCarl Expanded GAMS User Guide. Version 24.6. 2016. GAMS Development Corporation, Washington, DC, USA.
24. Makhorin A. GUSEK (GLPK Under Scite Extended Kit) 2012. Retrievable from:
gusek.sourceforge.net/gusek.html
25. Ferris M.C., Dirkse S.P., Jaglac J.H., Meeraus A. An extended mathematical programming framework // Computers and Chemical Engineering. 2009. Vol. 33. pp. 1973–1982.
26. Funaki K. 2009. State of the Art Survey of Commercial Software for Supply Chain Design. Georgia Institute of Technology. Retrievable from tli.isye.gatech.edu/research/supplychain/GTSCL_scdesignsoftware survey.pdf
27. Kantjukov R.A., Popov A.G., Ryzhenkov I.V., Gimranov R.K., Mustafin F.M., Modin V.K., Meshalkin V.P., Butusov O.B., Panarin V.M. Opyt razrabotki jenergoresursojeffektivnyh konstrukcij gazoprovodnyh sistem Respubliki Tatarstan s ispol'zovaniem polijetilenovyh trub // Sovremennye naukojomkie tehnologii. Regional'noe prilozhenie. – 2015. – № 1. – S. 112–119.
|