|
Sergey Dzuba,
Professor, Chair of Economic Theory and Finance
Irkutsk National Research Technical University
Irkutsk, Russian Federation
Once I ran into Serpent ‘normous and so a question quickly rose:
Where is the end of his great Neckie and where his Tailie went on forth?
I measured Serpent with a tape-line. The Answer ordinary was:
Where there’s the end of his great Neckie, then there his Tailie goes on forth.
Genrikh Sapgir
A properly prepared tool is not only convenient to work with, but also saves effort while performing the task with a higher quality. This completely applies to management and decision-making tools. The Power law, better known as the Pareto law, belongs to the category of widely known analysis methods used, probably, by one-tenth of its potential.
This paper outlines the class of analytical and management tasks, for which using the power law method may be effective. Along with the express analysis methods, I address some advanced methods that allows one to improve the power distribution up to the level of a professional tool.
Power Distribution, Pareto Law, and Zipf’s Law
Vilfredo Pareto himself has only indirect relation to the principle known as the Pareto Rule. One can only tell that, in the early 20-th century, when studying the distribution of personal income, he established that 20% of people accumulate 80% of the total income. Many years later, other researchers gave an image of a regularity to this observation that 20% of efforts bring 80% of result. In reality, the versatility and generality of this principle has a mythical character. Next, I refer to this Rule as 20/80, not to be confused with the Pareto law that has quite a different scientific content.
Starting with the work by the German physicist Felix Auerbach [1], one can observe an investigation into the sequence specific for the power distribution more definitely. If one assumes the biggest city in a fairly large state with a stable territory as 1, then the next city has the size of 1/2, with the following ones being 1/3, 1/4, etc. However, such a sequence is referred to as Zipf’s law by name of the American linguist George Zipf. He revealed the same pattern in the distribution of word-use frequencies in different languages and suggested that it possesses a universal character [2].
Generally, the power law distribution has the form:
 , (1) , (1)
where C is a constant,  is a distribution exponent. One can see that is a distribution exponent. One can see that 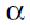 = 1 corresponds to the above description, which makes Zipf’s law a special case of the power law distribution. = 1 corresponds to the above description, which makes Zipf’s law a special case of the power law distribution.
The power-law sequence diagrammatic formulation is easy to visually confuse with any other rapidly growing (decreasing) sequence, for example, with the exponential law:
 . (2) . (2)
However, they are radically different in the logarithmic representation. Thus, for (2), one can see that, in the logarithmic scale, the exponential sequence would looks like a straight line, 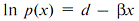 . Similarly, for the power sequence (1), the linear representation is in double logarithmic (log-log) axes(1) . Similarly, for the power sequence (1), the linear representation is in double logarithmic (log-log) axes(1) 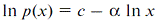 . These properties of the power and exponential distributions in the future are very useful for quick estimation. . These properties of the power and exponential distributions in the future are very useful for quick estimation.
The origin of the power behavior remains an open science problem. There are different types of mechanisms leading to it [3]. As a rule, this is the result of a complex interconnection among several processes. The most significant property of the power distribution is a relatively slow decrease in the sequence, resulting in a significant “mass” accumulation in the distribution “tail”(2). In contrast, the exponential distribution tail decreases very rapidly and all its mass is concentrated in the “head.”
From the above it follows that the nature of the power distribution contradicts the 20/80 Rule in that the main “mass” of the sequence is concentrated in its “head.” Nevertheless, some special cases (rather short sequences, or sequences with certain parameters, or if there is an exponential-like “tail”) probably might have parameters like this rule. Let us consider Zipf's law, for example. In a sequence of 1000 cities, one really gets the ratio close to 20/80. However, for 10,000 cities, this rule is wrong.
Recently, the interest to in the power-law distribution is has quickly grown. It appeared that it features a great number of quite different processes associated with human activity (the word-use frequency in the language, articles citing, the number of network relations, the number of books sold, etc.) and natural systems (earthquake magnitude, the size of moon craters, intensity of solar flares, etc.) [3]. Figure 1 shows the examples of such distributions like the Zipf plots(3).

Fig. 1 . Zipf plots of power law sequence examples. The data in the shaded regions do not correspond to the power law distribution. Source: [3].
Formally, (1) defines the distribution over the entire infinity interval, which causes problems with the finiteness of moments and normalization of the distribution. In practice, the power distribution might appear not throughout the all edges of data. Thus, in Figure 1b, only papers with citations over 100 have the power law. Similarly, there may be a situation, when not all data are available for a researcher, but only “the iceberg tip.” For example, one investigates a regularity for the size of firms having only the data from the Top-500 major companies. In this case, it is correct to speak of the power distribution with the observed minimal value
 , (3) , (3)
where  is the minimal value with the power distribution. In other words, one supposes that, for all is the minimal value with the power distribution. In other words, one supposes that, for all 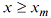 , the power law is true, but, for , the power law is true, but, for 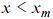 , there is either no data, or their distribution is not the power law. This two-parametric representation of power distribution (3) is termed the Pareto distribution. , there is either no data, or their distribution is not the power law. This two-parametric representation of power distribution (3) is termed the Pareto distribution.
In management, the power law distribution analysis is essential for tasks, in which one investigates the structure of an orderable population to a wide extent. Further, I address 3 cases in detail. In the first, a “population” of items is structured through the express analysis. This task is known as the ABC-analysis, and aims at determining the boundaries reasonably. In the second case, the ABC boundary estimation requires a more complex model approach, because it is not resolved through the express analysis. The third case presents how power-law distribution properties are used to solve some human resource management tasks. In all three cases, one can see that the 20/80 Rule is implemented nowhere, although empirical data have short series without heavy tails, i.e., they have prerequisites for its implementation.
Case 1: quick estimation of ABC boundaries
The task is to find the ABC boundaries as a part of the ABS-analysis process. In most cases, this task is solved “by eye” based on the researcher’s practical experience and intuition. This approach is under the pressure of the magic 20/80 Rule as a core of the ABC-analysis. For example, the Russian Wikipedia offers the (80:15:5)(5) boundaries, and, in the English Wiki, these boundaries are (75:25:5) or (67:23:10)(4). A rare researcher can oppose this magic, but there are such examples. Thus, the author in [5] refers only 50% of top items to the A-category, the B-category involves the items within the 50-80% range, and the rest was referred to the C-category.
The object of the investigation in Case 1 is a 942-item commodity set within the 100-1,655 RUB turnover range with the total turnover 67,194 mln RUB.
The fast estimation of the data is performed visually by a Zipf Plot. This can be done in MS Excel, for which one should do the following:
- Enter the data in a column, and sort them in the descending order.
- Display the sorted data as a Dot Plot chart. By default, the data in this column are output as the y-axis data.
- Select the Logarithmic scale option with the x- and y-axes.
Figure 2 shows the result. As compared to the classical Zipf Plot (see Fig. 1), the X and Y axes are swapped. To bring to a complete correspondence, one may perform another action:
- Add the rank column to the data table, and use it as the Y-axis source in the created diagram. The former y-axis data should be swapped as the x-axis data.
The last step is only optional as a tribute to pedantry(6). Henceforth, it is simpler to remember that one works with a swapped Zipf plot.

Fig.2 . Zipf Plot for the Case 1 commodity items. One can definitely see two segments (categories), A and B, with a power law distribution. Circles outline the boundaries of the segments.
The results in Fig. 2 confidently show that the distribution is not determined by the power law throughout all data. At the same time, it is divided into three segments quite clearly (the circles outline the boundaries):
1. The À-category includes first 60 commodity items(7) having the power-law distribution with a low exponent  . This means that this group features a slow decay rate, which leads to the fact that a small number of items have a significant mass. The lower boundary is expressed quite clearly as a “fracture” of the almost perfect straight line. . This means that this group features a slow decay rate, which leads to the fact that a small number of items have a significant mass. The lower boundary is expressed quite clearly as a “fracture” of the almost perfect straight line.
2. The B-category includes the items from 60 to (about) 500 also having a power-law distribution, but with a higher exponent 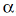 , then that for the A-category. This leads to a higher item value decay rate and requires much more items to accumulate a comparable mass. , then that for the A-category. This leads to a higher item value decay rate and requires much more items to accumulate a comparable mass.
3. The C-category includes the rest of the items with a distribution decaying exponentially or even faster, due to which its mass is very small.
Table 1 . Results of grouping for Case 1.
|
Category boundary |
Turnover, RUB, mln |
Share in turnover |
Share in items number |
Category À |
60 |
29,377 |
43,7% |
6,4% |
Category  |
500 |
34,115 |
50,8% |
46,7% |
Category Ñ |
942 |
3,703 |
5,5% |
46,9% |
Table 1 shows the consolidated results. It seems unusual that the A-category is less than the B-category. However, there is an objective substantiation for this indicating that the categories differ in the value decay rate.
Case 2: fit method for the ABC boundary estimation
The task for Case 1 is solved by the quick estimation method. However, life is not always so favorable. Fig. 3à displays the Zipf plot for the Case-2 commodity set, where (provisionally) the straight “head” and “tail” are connected by a very smooth curve without any hint of “fractures” at its gluing point as this was in the previous case. The middle of this sequence practically has an ideal exponential distribution, as one can realize by seeing this data in the logarithmic coordinates (Fig. 3b, see also Footnote 1).
One cannot visually find the point where the power-law “head” turns into the exponential-law “neck” (the boundary between the A- and B-categories). But it is more difficult to find the point where “the neck ends and the tail starts” on the exponential-like part of the curve (the boundary between the B- and C-categories). To solve these tasks, one should fit the distributions from the empirical data for the A and B ranges.

à) á)
Fig.3 . Case 2: a) Zipf plot (log-log), b) Log plot. The middle part of the data has an exponential distribution.
By using the Pareto distribution, one takes the index of value 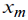 of the corresponding range lower boundary as m (3). Then, there is an estimation of the exponent of the corresponding range lower boundary as m (3). Then, there is an estimation of the exponent  by the maximum-likelihood technique [4]: by the maximum-likelihood technique [4]:
 . (4) . (4)
Estimation  is not the task, but it is helpful in searching for the is not the task, but it is helpful in searching for the 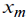 best approximation. One of simplest recommendations is varying best approximation. One of simplest recommendations is varying 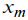 and observing and observing  that also varies significantly with the distribution nature variation [4]. However, further one will see that this simplest technique is not always successful. To avoid complicated statistical procedures, one may supplement it with a technique estimating the distance between fit and empirical sequences, as follows: that also varies significantly with the distribution nature variation [4]. However, further one will see that this simplest technique is not always successful. To avoid complicated statistical procedures, one may supplement it with a technique estimating the distance between fit and empirical sequences, as follows:
 , (5) , (5)
where õ are empirical values, and  are estimated ones. are estimated ones.
Fig. 4à demonstrates using (4)-(5) the best estimate for the fit distribution as the A-category low boundary within the m = [30..90] range. One can see that about m = 55, both estimations,  and D, grow dramatically due to an empirical distribution transformation. Therefore, one gets the nearest D minimum of this point at and D, grow dramatically due to an empirical distribution transformation. Therefore, one gets the nearest D minimum of this point at 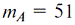 as the A-category ultimate boundary. as the A-category ultimate boundary.
Estimating the B-category low boundary is complicated, there is an attempt to approximate an exponential-like distribution by a power-law one. Visually, one cannot tell where this boundary may be, and, for that reason, the search is performed over a wide range. Fig. 4b demonstrates that the  variation occurs quite smoothly, and provides one with no information. But D jumps immediately after m = 280, therefore, if one wants to move the B-category boundary farthest right, this point is the best approximation. variation occurs quite smoothly, and provides one with no information. But D jumps immediately after m = 280, therefore, if one wants to move the B-category boundary farthest right, this point is the best approximation.

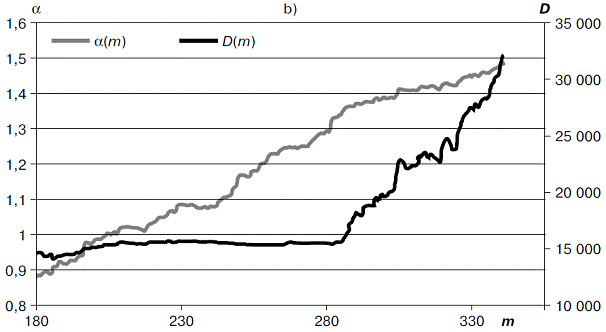
Fig. 4 . Estimating the low boundary for: a) À-category, b) Â-category.
Table 2 exhibits the final results of grouping.
Table 2 . Results of grouping for Case 2.
|
Category boundary |
Turnover, RUB, mln |
Share in turnover |
Share in items number |
Category À |
51 |
11,931 |
49,3% |
9,9% |
Category  |
280 |
10,753 |
44,5% |
44,6% |
Category Ñ |
514 |
1,504 |
6,2% |
45,5% |
Case 3: avoiding the lizard effect
The tasks like the “commodity” ABC-analysis may emerge in other fields, for example, in the human resources management. Suppose, one has a group of employees, whose performance is expressed numerically. This can be a KPI, or may be a cash equivalent return. Then, the performance of the employees can be ranked, and the task will be suitable to study the above-described analysis methods of a power-law distribution.
In Case 3, I consider a group of employees (48 persons) with the performance within the 0.2-2 mln RUB range. A fast estimation with a Zipf plot (see Fig. 5) shows that one possibly faces an exponential distribution (i.e., fast decrease) with a power-law “head”. The plot well evidences the structure of employees’ effectiveness with clear division between the leaders, middlings, and outsiders with the internal structure in the group of leaders. However, for a trained eye, this structure is visible in such a small group (although less explicitly) even on the normal plot.

Fig. 5 . Zipf plot for employees’ performance.
The illustrated structure may be a support for decision-making to improve the efficiency of the staff. The most obvious decision is dismissal of ineffective outsiders and efficiency increase from other groups. However, the knowledge of the properties of the ranked sequences suggests that the exponential “tail” is their essential attribute. Therefore, cutting the existing exponential “tail” off will lead to a “lizard effect”: the remaining part of the staff “makes” an exponential tail again, but at the expense of loosing the efficiency of the middlings' lower part.
If one speaks about a specific example, the argument about the “lizard effect” was understood by a HR Manager, which resulted in a more deliberate decision with selective dismissal of employees, and with the formation of a flexible reserve from the remaining personnel in case of a leave and temporary disability with the leaders and the middlings.
Another circumstance appeared to be in favor of such a decision. Economic calculations show that there is no wage fund saving after “cutting” the outsiders off. The basis for these calculations is the model with a careful staff performance recalculation. The model is based on the correction of the power-law distribution parameters.
Power-law: everywhere and nowhere
The power-law distribution generalizes such well-known phenomena as Zipf's law (power law with exponent α = 1) and the Pareto rule (the 20/80” Rule). A great number of identified man-made and natural processes lead to forming sequences with a power-law behavior. This creates an illusion that the Pareto rule is widespread and applied universally. In reality, the power-law distribution in its pure form is a rare phenomenon, and often occurs as a result of many complex processes effecting simultaneously. For example, the size ranking of firms has a power-law distribution in a very wide range. However, if one considers individual industries, there emerge exponential-like “tails.”
In practice of the commodity flows management, one deals only with fragments of larger and complex systems. Therefore, one should expect the power-law distribution to cover only a part of the data, possibly, the most important, where the strategic processes reached the required “density.” It is these examples that are presented in the Cases, where the power-law distribution features only the top part of the data. The breakpoints between the distribution parts are accepted as the À-, Â-, and Ñ-category boundaries.
The category boundary position (objective in the empirical distribution structure) may have subjective bases. Thus, the A-category cannot only be formed under demand factors, but, at the same time, as a result of a manager’s preferences concerning the operation convenience with individual commodity items, or their providers. Therefore, the formal acceptances stated in this paper should always be accompanied with a substantial analysis, in which one can find some anomalies, when individual items suddenly appear out of their category. The result of such an analysis should be not only the ABC estimation itself, but also a job setup for managers, for example, revealing the reasons for such anomalies and their elimination.
References
1. Auerbach F. Das Gesetz der Bevölkerungskonzentration // Petermanns Geographische Mitteilungen. 1913. 59, p. 74–76.
2. Zipf G.K. Human Behavior and the Principle of Least Effort // Addison-Wesley, Reading, MA. 1949.
3. Newman M.E. Power laws, Pareto distributions and Zipf's law // Contemporary physics. 2005. No. 46(5), p. 323-351.
4. Clauset A., Shalizi C.R., Newman M.E. Power-law distributions in empirical data // SIAM review. 2009. 51(4), p. 661-703.
5. Golovina T.A. Management of the foreign methods integration of the administrative analysis for the effectiveness estimation of the assortment policy in the pharmacy // Management In Russia and Abroad. 2009. No1.
(1) “Logarithmic scale” refers to the plot view replacing the vertical (ordinate) scale from normal to logarithmic. In the “log-log” view, two axes must have logarithmic scales.
(2) For example, biologists estimate the total mass of plankton in the ocean more than the total mass of whales. This means that if we tried to sort all the marine organisms by weight, then, most likely, this sequence would have the power distribution.
(3) “Zipf plot” is a special type of log-log scales plot diagram for the data sorted in the descending order, where the abscissa axis presents the value of a quantity, and the ordinate shows its sequence number (rank).
(4) ru.wikipedia.org/wiki/ABC-àíàëèç
(5) en.wikipedia.org/wiki/ABC_analysis
(6) In the classical Zipf plot, the rank is used as a probability that should be always presented on the y-axis.
(7) It is difficult to view it on the “paper version” of Fig. 2 due to the logarithmic scale. But the dots’ coordinates are visible in the pop-up label under the cursor in the MS Excel chart.
|


 , (3)
, (3) 

 . (4)
. (4) 

